(有)加賀スプリング製作所

 物体に荷重が掛かった時、物体は変形しますが
このとき変形前の形に対する変形の割合の事を「ひずみ」と言います。

 下記図を参照して頂ければ、材料の垂直方向に引張荷重が掛かれば、
その材料は縦に伸び、直角方向には縮み、圧縮荷重が掛かれば縦に縮まり、
直角方向に膨らみます。

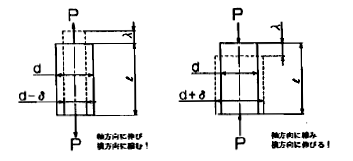
このとき荷重方向（軸方向）のひずみを縦ひずみといい、
荷重と直角方向（横方向）のひずみを横ひずみと言い、
縦ひずみをε、横ひずみε´とすると次の式で表わすことができます。

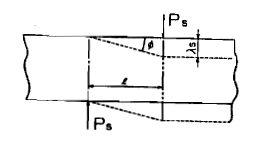
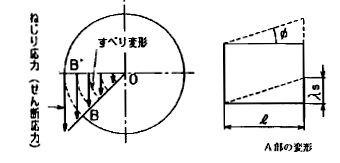
物体にせん断荷重が加えられるときは、下図の点線のように変形する。
このときのせん断ひずみγは下記のように示せます。

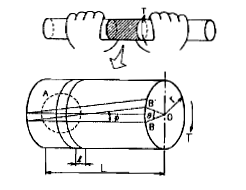
左下図のように棒をねじると、材料内部には応力とひずみが生じる。
ここで材料内部には右下図のようにせん断応力が生じていることが解ります。
このねじりによって生じるせん断力をねじり応力といいます。

せん断ひずみをγ、ねじり応力をτとすれば

せん断ひずみ　γ＝λs/ｌ＝tanΦ≒Φ[rad]
ねじり応力　　τ＝Gγ＝GΦ＝G・ｒθ/L
　　　　　　（：ｒθ＝LΦ）

[tag:せん断ひずみ ねじり応力]